题目描述#

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：

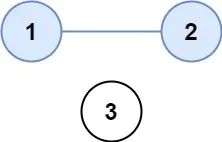
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

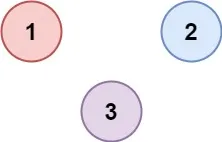
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

题解#

对连接的两点进行合并，最后求联通分量即可，为省份数量

class Solution {
    int[] parent;
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        parent = new int[n];
        for(int i = 0; i < n; i++) {
            parent[i] = i;
        }
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < i; j++) {
                if(isConnected[i][j] == 1) {
                    union(i, j);
                }
            }
        }
        int result = 0;
        for(int i = 0; i < n; i++) {
            if(parent[i] == i) {
                result++;
            }
        }
        return result;
    }

    public void union(int x, int y) {
        parent[find(x)] = find(y);
    }

    public int find(int num) {
        if(parent[num] != num) {
            parent[num] = find(parent[num]);
        }
        return parent[num];
    }
}

题目描述#

给定一个长度为 n 的整数数组 nums ，其中 nums 是范围为 [1，n] 的整数的排列。还提供了一个 2D 整数数组 sequences ，其中 sequences[i] 是 nums 的子序列。 检查 nums 是否是唯一的最短 超序列 。最短 超序列 是 长度最短 的序列，并且所有序列 sequences[i] 都是它的子序列。对于给定的数组 sequences ，可能存在多个有效的 超序列 。

• 例如，对于 sequences = [[1,2],[1,3]] ，有两个最短的 超序列 ，[1,2,3] 和 [1,3,2] 。
• 而对于 sequences = [[1,2],[1,3],[1,2,3]] ，唯一可能的最短 超序列 是 [1,2,3] 。[1,2,3,4] 是可能的超序列，但不是最短的。

如果 nums 是序列的唯一最短 超序列 ，则返回 true ，否则返回 false 。 子序列 是一个可以通过从另一个序列中删除一些元素或不删除任何元素，而不改变其余元素的顺序的序列。

示例 1：

输入：nums = [1,2,3], sequences = [[1,2],[1,3]]
输出：false
解释：有两种可能的超序列：[1,2,3]和[1,3,2]。
序列 [1,2] 是[1,2,3]和[1,3,2]的子序列。
序列 [1,3] 是[1,2,3]和[1,3,2]的子序列。
因为 nums 不是唯一最短的超序列，所以返回false。

示例 2：

输入：nums = [1,2,3], sequences = [[1,2]]
输出：false
解释：最短可能的超序列为 [1,2]。
序列 [1,2] 是它的子序列：[1,2]。
因为 nums 不是最短的超序列，所以返回false。

示例 3：

输入：nums = [1,2,3], sequences = [[1,2],[1,3],[2,3]]
输出：true
解释：最短可能的超序列为[1,2,3]。
序列 [1,2] 是它的一个子序列：[1,2,3]。
序列 [1,3] 是它的一个子序列：[1,2,3]。
序列 [2,3] 是它的一个子序列：[1,2,3]。
因为 nums 是唯一最短的超序列，所以返回true。

题解#

思路类似于课程表，存储其出度入度，在每一次循环中判断queue元素是否大于1，大于则返回true

class Solution {
    public boolean sequenceReconstruction(int[] nums, int[][] sequences) {
        int n = nums.length;
        int[] before = new int[n + 1];
        Set<Integer>[] after = new Set[n + 1];
        for(int i = 1; i <= n; i++) {
            after[i] = new HashSet<Integer>();
        }
        for(int i = 0; i < sequences.length; i++) {
            for(int j = 0; j < sequences[i].length - 1; j++) {
                int prev = sequences[i][j];
                int next = sequences[i][j + 1];
                before[next]++;
                after[prev].add(next);
            }
        }
        Queue<Integer> queue = new LinkedList<>();
        for(int i = 1; i <= n; i++) {
            if(before[i] == 0) {
                queue.offer(i);
            }
        }
        while(!queue.isEmpty()) {
            if(queue.size() > 1) {
                return false;
            }
            int num = queue.poll();
            Set<Integer> set = after[num];
            for(int next : set) {
                before[next]--;
                if(before[next] == 0) {
                    queue.offer(next);
                }
            }
        }
        return true;

    }
}