题目描述#

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1：

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

示例 2：

输入：nums = [0,3,7,2,5,8,4,6,0,1]
输出：9

示例 3：

输入：nums = [1,0,1,2]
输出：3

题解#

解法一：排序后遍历 O(nlogn)

将整个数组用sort排序，在遍历的过程中判断当前数是否符合连续，如果不连续将count重置为1，如果符合条件count自增并且迭代result

还需要注意当存在重复数字的时候我们需要将其跳过，不然也不符合条件（实际上是符合的，因为可以不取同样的数字）

class Solution {
    public int longestConsecutive(int[] nums) {
        if (nums == null || nums.length == 0) {
            return 0;
        }
        Arrays.sort(nums);
        int result = 1;
        int count = 1;
        for (int i = 1; i < nums.length; i++) {
            if(nums[i] == nums[i - 1]) {
                continue;
            }
            if (nums[i - 1] + 1 == nums[i]) {
                count++;
                result = Math.max(result, count);
            } else {
                count = 1;
            }
        }
        return result;
    }
}

解法二：Set集合遍历

将数组中的元素放入Set集合中，去重并且便于后续使用contains快速判断是否存在目标数字

遍历Set中的数字num，仅当Set中不存在 num - 1 的时候（说明如果将其包含在连续序列中的时候其为序列的起始位置），此时将起始的数字用current记录，并将计数器count设置为1，我们从Set中依次寻找是否存在current + 1，如果没有证明该起始位置的序列结束，用count迭代result，如果存在则继续判断下去

class Solution {
    public int longestConsecutive(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for(int num : nums) {
            set.add(num);
        }
        int result = 0;
        for(int num : set) {
            if(set.contains(num - 1)) {
               continue; 
            }
            int currentNum = num;
            int count = 1;
            while(set.contains(currentNum + 1)) {
                count++;
                currentNum++;
            }
            result = Math.max(result, count);
        }
        return result;
    }
}

这种解决方式的时间复杂度是O(n)，虽然用了两层循环，但是因为只选取各个连续子序列的起始元素，在所有的内层循环中每个数字只会被遍历一次

题目描述#

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

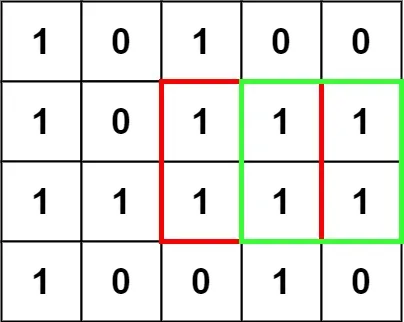
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

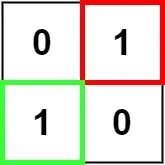
输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

题解#

class Solution {
    public int maximalSquare(char[][] matrix) {
        if(matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }
        int row = matrix.length;
        int col = matrix[0].length;
        int result = 0;
        int[][] dp = new int[row + 1][col + 1];
        for(int i = 0; i < row; i++) {
            for(int j = 0; j < col; j++) {
                if(matrix[i][j] == '1') {
                    dp[i + 1][j + 1] = Math.min(Math.min(dp[i + 1][j], dp[i][j + 1]), dp[i][j]) + 1;
                    result = Math.max(result, dp[i + 1][j + 1]); 
                }
            }
        }
        return result * result;
    }
}