题目描述#

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

题解#

回溯法：

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> list = new ArrayList<>();
    public List<List<Integer>> permute(int[] nums) {
        int n = nums.length;
        for(int num : nums) {
            list.add(num);
        }
        fun(n, 0);
        return result;
    }

    public void fun(int n, int index) {
        if(n == index) {
            result.add(new ArrayList<>(list));
            return;
        }
        for(int i = index; i < n; i++) {
            Collections.swap(list, i, index);
            fun(n, index + 1);
            Collections.swap(list, i, index);
        }
    }
}

题目描述#

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

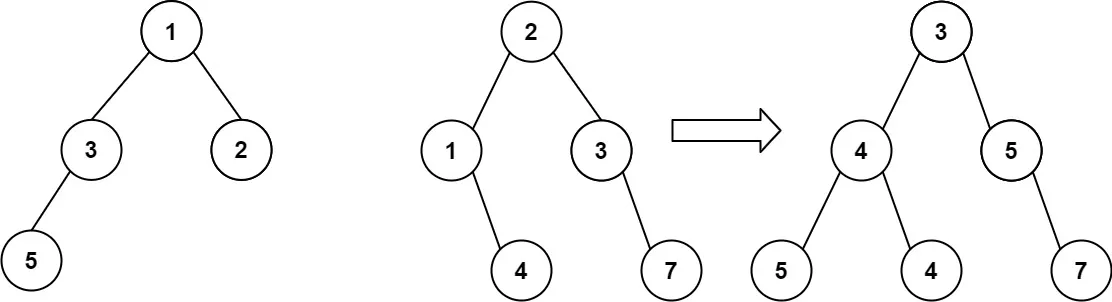
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

题解#

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1 == null) {
            return root2;
        }
        if(root2 == null) {
            return root1;
        }
        TreeNode merge = new TreeNode();
        merge.val = root1.val + root2.val;
        merge.left = mergeTrees(root1.left, root2.left);
        merge.right = mergeTrees(root1.right, root2.right);
        return merge;      
    }
}

题目表述#

给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数 ，返回一个长度为 n + 1 的数组 ans 作为答案。

示例 1：

输入：n = 2
输出：[0,1,1]
解释：
0 --> 0
1 --> 1
2 --> 10

示例 2：

输入：n = 5
输出：[0,1,1,2,1,2]
解释：
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101

题解#

解法一：用之前汉明距离的函数进行循环赋值，可以很轻松的实现，但是时间复杂度较高在n的循环中需要套嵌一层log n来求解对应数字的含1数量

class Solution {
    public int[] countBits(int n) {
        int[] result = new int[n + 1];
        for(int i = 0; i <= n; i++) {
            result[i] = count(i);
        }
        return result;
    }

    public int count(int num) {
        int result = 0;
        while(num != 0) {
            result += (1 & num);
            num = num >> 1;
        }
        return result;
    }
}

解法二：动态规划求解

对于每一个数字分为两种情况，末位不为1的情况下，它所对应的结果应该和之前求解出的num >> 1相同，而对于末尾为1的时候，结果应该是上述得出结果num - 1的1的总和结果加上末尾的1

class Solution {
    public int[] countBits(int n) {
        int[] result = new int[n + 1];
        for(int i = 0; i <= n; i++) {
            if((i & 1) == 0) {
                result[i] = result[i >> 1];
            } else {
                result[i] = result[i - 1] + 1;
            }
        }
        return result;
    }
}

可以将时间复杂度降至O(n)