题目描述#

假设 力扣（LeetCode）即将开始 IPO 。为了以更高的价格将股票卖给风险投资公司，力扣 希望在 IPO 之前开展一些项目以增加其资本。 由于资源有限，它只能在 IPO 之前完成最多 k 个不同的项目。帮助 力扣 设计完成最多 k 个不同项目后得到最大总资本的方式。

给你 n 个项目。对于每个项目 i ，它都有一个纯利润 profits[i] ，和启动该项目需要的最小资本 capital[i] 。

最初，你的资本为 w 。当你完成一个项目时，你将获得纯利润，且利润将被添加到你的总资本中。

总而言之，从给定项目中选择 最多 k 个不同项目的列表，以 最大化最终资本 ，并输出最终可获得的最多资本。

答案保证在 32 位有符号整数范围内。

示例 1：

输入：k = 2, w = 0, profits = [1,2,3], capital = [0,1,1]
输出：4
解释：
由于你的初始资本为 0，你仅可以从 0 号项目开始。
在完成后，你将获得 1 的利润，你的总资本将变为 1。
此时你可以选择开始 1 号或 2 号项目。
由于你最多可以选择两个项目，所以你需要完成 2 号项目以获得最大的资本。
因此，输出最后最大化的资本，为 0 + 1 + 3 = 4。

示例 2：

输入：k = 3, w = 0, profits = [1,2,3], capital = [0,1,2]
输出：6

题解#

将成本与纯利益放置一个二维数组中，将其对应，再按照成本从小到大排序，保证成本能满足后面的项目放入heap的话前面的也能

循环k次，在累加利益之前，放入所有成本能够满足的项目，项目用current标识，之后用heap取出最大的利益项目迭代资本w

class Solution {
    public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {
        int n = profits.length;
        int[][] arr = new int[n][2];
        for(int i = 0; i < n; i++) {
            arr[i][0] = capital[i];
            arr[i][1] = profits[i];
        }
        Arrays.sort(arr, (a, b) -> a[0] - b[0]);
        PriorityQueue<Integer> heap = new PriorityQueue<>((a, b) -> b - a);
        int current = 0;
        for(int i = 0; i < k; i++) {
            while(current < n && arr[current][0] <= w) {
                heap.add(arr[current][1]);
                current++;
            }
            if(!heap.isEmpty()) {
                w += heap.poll();
            } else {
                break;
            }
        }
        return w;
    }
}

题目描述#

树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

示例 1：

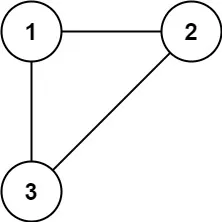
输入: edges = [[1,2],[1,3],[2,3]]
输出: [2,3]

示例 2：

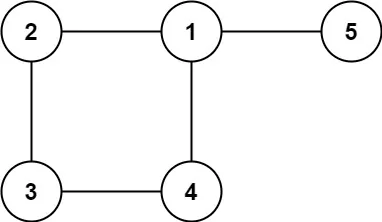
输入: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
输出: [1,4]

题解#

并查集，查找第一个能形成环的边，如果find的两个结果是一样的则代表两个数字已经连接，这条边是冗余的，如果不一样，则合并两个图union一下

class Solution {
    int[] parent;
    public int[] findRedundantConnection(int[][] edges) {
        int n = edges.length;
        parent = new int[n + 1];
        for(int i = 1; i <= n; i++) {
            parent[i] = i;
        }
        for(int[] edge : edges) {
            int x = edge[0];
            int y = edge[1];
            if(find(x) == find(y)) {
                return edge;
            } else {
                union(x, y);
            }
        }
        return new int[0];
    }

    int find(int index) {
        if(parent[index] != index) {
            parent[index] = find(parent[index]);
        }
        return parent[index];
    }

    void union(int x, int y) {
        parent[find(x)] = find(y);
    }
}