822 字
4 分钟
LeetCode刷题(路径总和III、零钱兑换)
路径总和III
题目描述
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。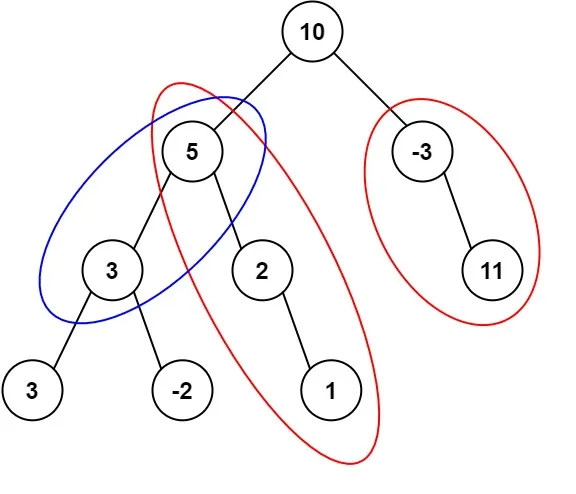
示例 1:
输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出:3
解释:和等于 8 的路径有 3 条,如图所示。示例 2:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:3题解
题解和和为k的子数组次数思路一致,将数据结构更换为了二叉树,我们还是使用前缀和+哈希表的方式求解,全局定义一个存储前缀和的哈希表,依次通过dfs的方式遍历左右节点,最后回溯删除当前节点的前缀和情况防止对于其他路径进行干扰
class Solution {
Map<Long, Integer> map = new HashMap<>();
public int pathSum(TreeNode root, int targetSum) {
map.put(0L, 1);
return dfs(root, 0L, targetSum);
}
public int dfs(TreeNode root, long preSum, int targetSum) {
if(root == null) {
return 0;
}
int result = 0;
preSum += root.val;
long target = preSum - targetSum;
result += map.getOrDefault(target, 0);
map.put(preSum, map.getOrDefault(preSum, 0) + 1);
result += dfs(root.left, preSum, targetSum);
result += dfs(root.right, preSum, targetSum);
map.put(preSum, map.get(preSum) - 1);
return result;
}
}零钱兑换
题目描述
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1示例 2:
输入:coins = [2], amount = 3
输出:-1示例 3:
输入:coins = [1], amount = 0
输出:0题解
解法一 回溯法(超时)
我一看到这一题,我就想这不是做过嘛,回溯法直接秒,遍历一下之前的结果即可,果不其然时间效率惨淡(39/189)
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> list = new ArrayList<>();
public int coinChange(int[] coins, int amount) {
dfs(coins, amount, 0);
if(result.size() == 0) {
return -1;
}
int target = Integer.MAX_VALUE;
for(int i = 0; i < result.size(); i++) {
List<Integer> currentList = result.get(i);
target = Math.min(target, currentList.size());
}
return target;
}
public void dfs(int[] coins, int amount, int index) {
if(index == coins.length) {
return;
}
if(amount == 0) {
result.add(new ArrayList<>(list));
return;
}
dfs(coins, amount, index + 1);
int newNum = coins[index];
int newTarget = amount - newNum;
if(newNum <= amount) {
list.add(newNum);
dfs(coins, newTarget, index);
list.remove(list.size() - 1);
}
}
}看了下题解应该使用动态规划完成,不然在不限制硬币数量的时候,复杂度随amount指数增长,就太夸张了
解法二:动态规划
建立一个amount + 1大小的int数组其中存放到这个下表的最小硬币数量,逐个遍历,对每个目标i循环中遍历coins数组,当不超过i时,更新min最小硬币数量(用dp[i - coins[i]] + 1进行迭代min)
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
for(int i = 1; i <= amount; i++) {
for(int coin : coins) {
if(i >= coin && dp[i - coin] != Integer.MAX_VALUE) {
dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
}
}
}
return dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount];
}
} LeetCode刷题(路径总和III、零钱兑换)
https://thrinisty.github.io/Blog/posts/leetcode刷题路径总和iii零钱兑换/ 
