矩阵中的最长递增路径#

题目描述#

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

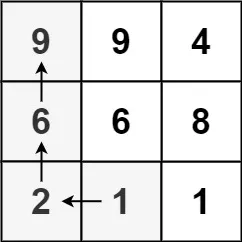
输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4 
解释：最长递增路径为 [1, 2, 6, 9]。

示例 2：

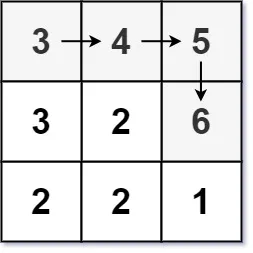
输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4 
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：

输入：matrix = [[1]]
输出：1

题解#

用dfs深度搜索，分别向上下左右寻找，从当前位置出发满足条件的最长路径，用最长的路径加上原始的1返回即可

class Solution {
    public int longestIncreasingPath(int[][] matrix) {
        int result = 0;
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                result = Math.max(result, dfs(matrix, i, j, Integer.MIN_VALUE));
            }
        }
        return result;
    }

    public int dfs(int[][] matrix, int x, int y, int prev) {
        if (x >= 0 && x < matrix.length && y >= 0 && y < matrix[0].length) {
            int num = matrix[x][y];
            if (num > prev) {
                int u = dfs(matrix, x - 1, y, num);
                int d = dfs(matrix, x + 1, y, num);
                int l = dfs(matrix, x, y - 1, num);
                int r = dfs(matrix, x, y + 1, num);
                int max = Math.max(Math.max(u, d), Math.max(l, r));
                return max + 1;
            }
            return 0;
        }
        return 0;
    }
}

但是这种方式出现超时，因为到每一个位置都需要重新计算该位置出发时的最长长度，我们用dp二维数组作为记忆，需要求该位置最长长度优先查记忆即可

class Solution {
    int[][] dp;

    public int longestIncreasingPath(int[][] matrix) {
        int result = 0;
        dp = new int[matrix.length][matrix[0].length];
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                result = Math.max(result, dfs(matrix, i, j, Integer.MIN_VALUE));
            }
        }
        return result;
    }

    public int dfs(int[][] matrix, int x, int y, int prev) {
        if (x >= 0 && x < matrix.length && y >= 0 && y < matrix[0].length) {
            int num = matrix[x][y];
            if (num > prev) {
                if(dp[x][y] > 0) {
                    return dp[x][y];
                }
                int u = dfs(matrix, x - 1, y, num);
                int d = dfs(matrix, x + 1, y, num);
                int l = dfs(matrix, x, y - 1, num);
                int r = dfs(matrix, x, y + 1, num);
                int max = Math.max(Math.max(u, d), Math.max(l, r));
                dp[x][y] = max + 1;
                return max + 1;
            }
            return 0;
        }
        return 0;
    }
}