题目描述#

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（从第 0 层开始），则该层包含 1~ 2h 个节点。

示例 1：

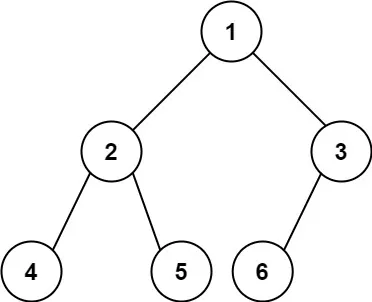
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

提示：

• 树中节点的数目范围是[0, 5 * 104]
• 0 <= Node.val <= 5 * 104
• 题目数据保证输入的树是 完全二叉树

**进阶：**遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

题解#

解法一：通过递归求解，时间复杂度为O(n)，没有用到二叉树的性质

class Solution {
    public int countNodes(TreeNode root) {
        if(root == null) return 0;
        int left = countNodes(root.left);
        int right = countNodes(root.right);
        return left + right + 1;
    }
}

解法二：计算所有两侧的层高，如果相同则代表左树是满二叉树，节点个数为1 << left，还需要算右数的节点数

如果层高不同则代表右树是满二叉树，还需要计算左侧的满二叉树节点数量，将结果相加

class Solution {
    public int countNodes(TreeNode root) {
        if(root == null) return 0;
        int left = countLevel(root.left);
        int right = countLevel(root.right);
        if(left == right) {
            return (1 << left) + countNodes(root.right);
        } else {
            return countNodes(root.left) + (1 << right);
        }
    }

    public int countLevel(TreeNode root) {
        int level = 0;
        while(root != null) {
            level++;
            root = root.left;
        }
        return level;
    }
}

题目描述#

给定一个二叉树：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

初始状态下，所有 next 指针都被设置为 NULL 。

示例 1：

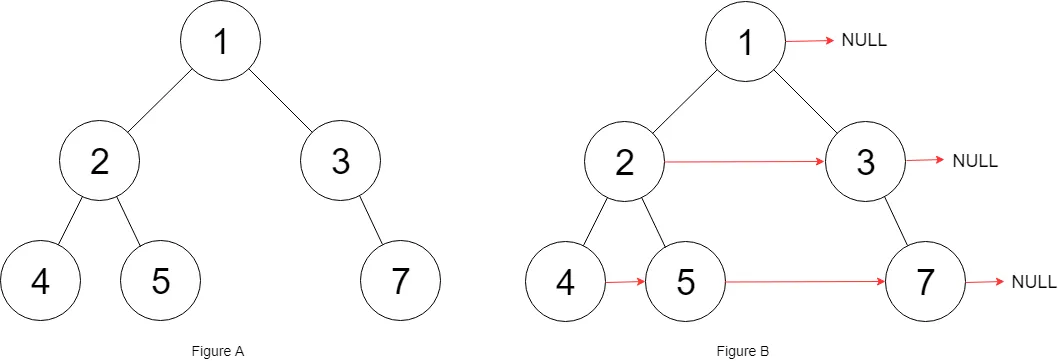
输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。

示例 2：

输入：root = []
输出：[]

题解#

运用层序遍历，将每一层的元素顺次链接即可

class Solution {
    public Node connect(Node root) {
        if(root == null) return null;
        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()) {
            int n = queue.size();
            for(int i = 0; i < n; i++) {
                Node node = queue.poll();
                if(i < n - 1) {
                    node.next = queue.peek();
                }
                if(node.left != null) queue.offer(node.left);
                if(node.right != null) queue.offer(node.right);
            }
        }
        return root;   
    }
}

题目描述#

实现一个二叉搜索树迭代器类BSTIterator ，表示一个按中序遍历二叉搜索树（BST）的迭代器：

• BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字，且该数字小于 BST 中的任何元素。
• boolean hasNext() 如果向指针右侧遍历存在数字，则返回 true ；否则返回 false 。
• int next()将指针向右移动，然后返回指针处的数字。

注意，指针初始化为一个不存在于 BST 中的数字，所以对 next() 的首次调用将返回 BST 中的最小元素。

你可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 的中序遍历中至少存在一个下一个数字。

示例：

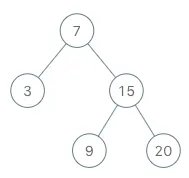
输入
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
输出
[null, 3, 7, true, 9, true, 15, true, 20, false]

解释
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next();    // 返回 3
bSTIterator.next();    // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 20
bSTIterator.hasNext(); // 返回 False

题解#

运用栈来进行状态存储

先回顾一下中序遍历的非递归方式

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode p = root;
        while(!stack.isEmpty() || p != null) {
            while(p != null) {
                stack.push(p);
                p = p.left;
            }
            p = stack.pop();
            result.add(p.val);
            p = p.right;
        }
        return result;
    }
}

更改为迭代器的方式

class BSTIterator {
    Stack<TreeNode> stack = new Stack<>();
    TreeNode p;

    public BSTIterator(TreeNode root) {
        p = root;
    }
    
    public int next() {
        while(p != null) {
            stack.push(p);
            p = p.left;
        }
        TreeNode target = stack.pop();
        p = target.right;
        return target.val;
    }

    
    public boolean hasNext() {
        return !stack.isEmpty() || p != null;
    }
}