克隆图
题目描述
给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
class Node {
public int val;
public List<Node> neighbors;
}测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1:
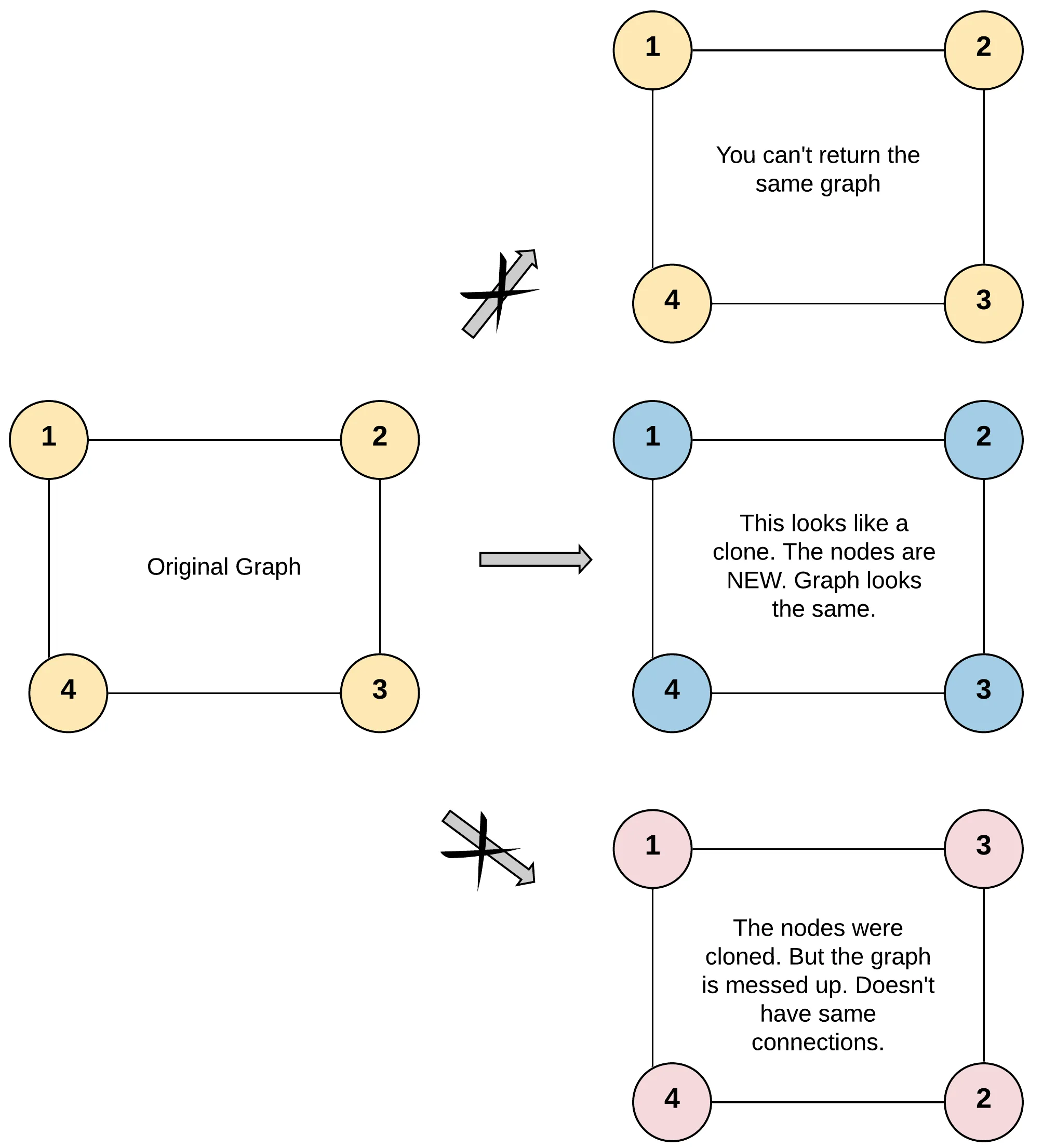
输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。示例 2:
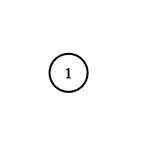
输入:adjList = [[]]
输出:[[]]
解释:输入包含一个空列表。该图仅仅只有一个值为 1 的节点,它没有任何邻居。示例 3:
输入:adjList = []
输出:[]
解释:这个图是空的,它不含任何节点。题解
建立一个map集合,被复制节点为key,复制后的节点作为value
如果当前节点被复制过,则从map中取出复制的节点直接返回
如果没有则创建复制节点并放入map集合中,之后将邻居节点复制后放入List中,最后返回复制后的节点
class Solution {
Map<Node, Node> map = new HashMap<>();
public Node cloneGraph(Node node) {
if(node == null) return null;
Node newNode = map.get(node);
if(newNode != null) return newNode;
newNode = new Node(node.val, new ArrayList<>());
map.put(node, newNode);
for(Node next : node.neighbors) {
newNode.neighbors.add(cloneGraph(next));
}
return newNode;
}
}课程表Ⅱ
题目描述
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。
- 例如,想要学习课程
0,你需要先完成课程1,我们用一个匹配来表示:[0,1]。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:[0,1]
解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。示例 2:
输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出:[0,2,1,3]
解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。示例 3:
输入:numCourses = 1, prerequisites = []
输出:[0]题解
按照课程表方法,在位0的时候加入课程即可
class Solution {
public int[] findOrder(int numCourses, int[][] prerequisites) {
int n = prerequisites.length;
int[] before = new int[numCourses];
List<Integer>[] after = new List[numCourses];
List<Integer> result = new ArrayList<>();
for(int i = 0; i < numCourses; i++) {
after[i] = new LinkedList<>();
}
for(int rule[] : prerequisites) {
before[rule[0]]++;
after[rule[1]].add(rule[0]);
}
Queue<Integer> queue = new LinkedList<>();
int count = 0;
for(int i = 0; i < numCourses; i++) {
if(before[i] == 0) {
queue.offer(i);
result.add(i);
}
}
while(!queue.isEmpty()) {
int target = queue.poll();
List<Integer> nextList = after[target];
for(int next : nextList) {
before[next]--;
if(before[next] == 0) {
queue.offer(next);
result.add(next);
}
}
count++;
}
if(count != numCourses) return new int[0];
int[] target = new int[numCourses];
for(int i = 0; i < numCourses; i++) {
target[i] = result.get(i);
}
return target;
}
}除法求值
题目描述
给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串,也需要用 -1.0 替代这个答案。
**注意:**输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
**注意:**未在等式列表中出现的变量是未定义的,因此无法确定它们的答案。
示例 1:
输入:equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出:[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释:
条件:a / b = 2.0, b / c = 3.0
问题:a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果:[6.0, 0.5, -1.0, 1.0, -1.0 ]
注意:x 是未定义的 => -1.0示例 2:
输入:equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]
输出:[3.75000,0.40000,5.00000,0.20000]示例 3:
输入:equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]
输出:[0.50000,2.00000,-1.00000,-1.00000]题解
用map存储各个路径以及对应权重,利用弗洛伊德算法求解所有的可能,最后看是否存在其中返回结果即可
class Solution {
Map<String, Double> map = new HashMap<>();
Set<String> set = new HashSet<>();
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
for(int i = 0; i < equations.size(); i++) {
String a = equations.get(i).get(0);
String b = equations.get(i).get(1);
map.put(a + " " + b, values[i]);
map.put(b + " " + a, 1.0 / values[i]);
set.add(a);
set.add(b);
}
for(String a : set) map.put(a + " " + a, 1.0);
for(String k : set) {
for(String i : set) {
for(String j : set) {
if(map.containsKey(i + " " + j)) continue;
if(map.containsKey(i + " " + k) && map.containsKey(k + " " + j)) {
map.put(i + " " + j, map.get(i + " " + k) * map.get(k + " " + j));
}
}
}
}
double[] result = new double[queries.size()];
for(int i = 0; i < queries.size(); i++) {
String a = queries.get(i).get(0);
String b = queries.get(i).get(1);
if(map.containsKey(a + " " + b)) {
result[i] = map.get(a + " " + b);
} else {
result[i] = -1.0;
}
}
return result;
}
}
