题目描述#

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回左上角 (row1, col1) 、右下角 (row2, col2) 的子矩阵的元素总和。

示例 1：

输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]]);
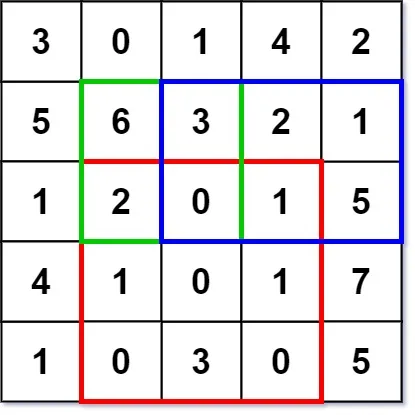
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

题解#

在初始化数组的时候计算出整个数组每行的前缀和，在后续计算区间内的时候只需要对于每一行进行计算求和（利用前缀和二维数组）相加返回即可

class NumMatrix {
    int[][] preSum;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        preSum = new int[m][n + 1];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                preSum[i][j + 1] = preSum[i][j] + matrix[i][j];
            }
        }

    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;
        for (int i = row1; i <= row2; i++) {
            sum += preSum[i][col2 + 1] - preSum[i][col1];
        }
        return sum;
    }
}

题目描述#

给定一个非负整数 *numRows，*生成「杨辉三角」的前 numRows 行。

在**「杨辉三角」**中，每个数是它左上方和右上方的数的和。

示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

题解#

创建数组，初始化1，动态添加每一行的元素即可，最后放入List中返回

class Solution {
    public List<List<Integer>> generate(int numRows) {
        int[][] arr = new int[numRows][];
        for(int i = 0; i < numRows; i++) {
            arr[i] = new int[i + 1];
            arr[i][0] = 1;
            arr[i][i] = 1;
        }
        for(int i = 2; i < numRows; i++) {
            for(int j = 1; j < i; j++) {
                arr[i][j] = arr[i - 1][j] + arr[i - 1][j - 1];
            }
        }
        List<List<Integer>> result = new ArrayList<>();
        for(int i = 0; i < numRows; i++) {
            List<Integer> list = new ArrayList<>();
            for(int j = 0; j <= i; j++) {
                list.add(arr[i][j]);
            }
            result.add(list);
        }
        return result;
    }
}